The first step in finding the big O of a complexity function is to remove all terms except the one with the highest growth rate. To be able to do that, we must know the growth rate of some common functions. In the following figure, we have plotted some of the most common functions:
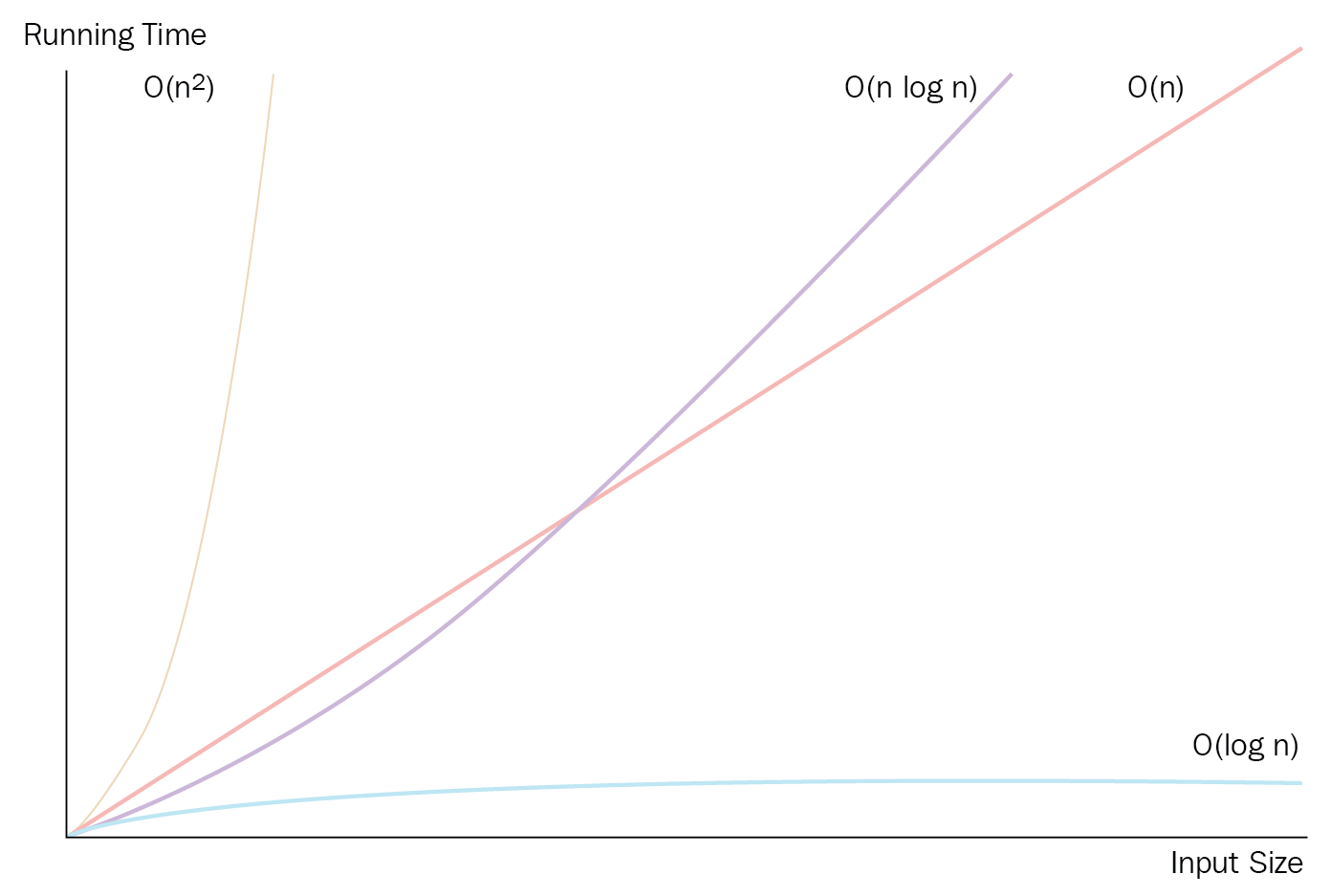
The growth rates are independent of machine or coding style and so on, when the growth rates differ between two algorithms, the one with the slowest growth rate will always win when the input size gets sufficiently large. Let’s see what happens with the running time for different growth rates if we assume that it takes 1 ms to perform 1 unit of work. The following table lists the growth function, its common name, and different input sizes, n:
| f(n) | Name | n = 10 | n = 50 | n = 100 |
|---|---|---|---|---|
| O(1) | Constant | 0.001 sec | 0.001 sec | 0.001 sec |
| O(log n) | Logarithmic | 0.003 sec | 0.006 sec | 0.01 sec |
| O(n) | Linear | 0.01 sec | 0.05 sec | 1 sec |
| O(n log n) | Linearithmic or n log n | 0.03 sec | 0.3 sec | 10 sec |
| O(n2) | Quadratic | 0.1 sec | 2.5 sec | 16.7 minutes |
| O(2n) | Exponential | 1 sec | 357 centuries | Inf |